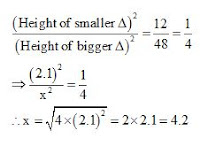SSC Quiz : Quantitative Aptitude | 09 - 01 - 18

In SSC exam quantitative Aptitude section is more scoring and easy if you know the shorts tricks and formulas of all the topic. So, it is important to know the basic concept of all the topic so you can apply the short tricks and solve the question with the new concept in lesser time while giving the quiz. It will help you to score more marks from this section in less time period. Quantitative Aptitude section basically measures your mathematical and calculation approach of solving the question. SSC Quiz Of quantitative Aptitude section helps you to analysis your preparation level for upcoming SSC examination. Mahendra Guru provides you Quantitative Aptitude Quiz for SSC examination based on the latest pattern. So that you can practice on regular basis. It will definitely help you to score good marks in the exam. It is the most important section for all the govt exam like Insurance, SSC-MTS, CGL, CHSL, State Level, and other Competitive exams.

You can clear your doubts before exam. Mahendra Guru also provides you an important note and study material for all subject and test through its website, Mahendra Guru App and YouTube channel apart from it Speed Test Portal. Most of these preparation products are also available for purchase on my shop. You can also visit Mahendras.org to get more information about our endeavour for your success. You can also study in details through our E-Mahendras Facebook and Mahendra Guru YouTube channel of Quantitative Aptitude.   

Q.1 – What is the maximum value of sin 3θ cos 2θ + cos 3θ sin 2θ?

           sin 3θ cos 2θ + cos 3θ sin 2θ का अधिकतम मान क्या होगा ?

(A) 1

(B) 2

(C) 4

(D) 10

Sol. – (A)

sin 3 θ cos 2 θ + cos 3 θ sin 2 θ = sin (3θ + 2θ)= sin 5 θ
maximum/अधिकतम = 1

Q.2 – 288 meter railing need the fencing the boundary of semicircular park. Then find the area of park?

एक अर्द्ध वृत्ताकार पार्क में बाड़ लगाने के लिए 288 मीटर रेलिंग की आवश्यकता है। पार्क का क्षेत्रफल बताइए।

(A) 6589 m²./ मी²

(B) 9865 m²./ मी²

(C) 8956 m²./ मी²

(D) 4928 m²./ मी²

Sol. – (D)

πr + 2r = 288
 r = ×7= 56
 Area/क्षेत्रफल = = 4928 m². / मी²

Q.3 – The angle of elevation of a tower at level ground is 30^o. The angle of elevation become θ, when moved 20 m. towards the tower. If the height is   m., then what is θ equal to?

किसी मीनार का समतल पर उन्नयन कोण 30^o है। मीनार की तरफ 20 मीटर चलने पर उन्नयन कोण θ हो जाता है। यदि मीनार की ऊँचाई मी. हो तो θ किसके बराबर होगा?

(A) 45^o

(B) 60^o

(C) 75^o

(D) None of these/इनमें से कोई नहीं

Sol. – (B)

Q.4 – Satya starts business with Rs.5000 and after 4 months, Subhash joins with Satya as his partner, after a year, the profit is divided in the ratio 2:1 respectively. What is Subhash's contribution in the capital?

सत्या रू 5000 से एक व्यवसाय शुरू करता है और 4 माह बाद सुभाष सत्या के साझीदार के रूप में जुड़ता है। एक वर्ष बाद लाभ को क्रमशः 2 : 1 के अनुपात में बांटा जाता है, तो पूंजी में सुभाष का योगदान कितना है?

(A) Rs. /रु.3600

(B) Rs. /रु.3700

(C) Rs. /रु.3750

(D) Rs. /रु.3800

Sol. – (C)

Let Subhash contribution in the capital be x/ माना पूंजी में सुभाष का योगदान x रू. है।

x =
x = Rs./रु. 3750

Q.5 – A solid metallic cylinder of base 3 cm and height 5 cm is melted to make a solid cones of height 1 cm and base radius 1 mm. The value of n is-

3सेमी आधार और 5 सेमी ऊँचाई वाले एक ठोस धात्विक बेलन को गलाकर 1 सेमी ऊँचाई और 1 मिमी आधार त्रिज्या वाले n ठोस शंकु बनाये जाते हैं। n का मान है-

(A) 450

(B) 1350

(C) 4500

(D) 13500

Sol. – (D)

= 13500

Q.6 – ABCD is a cyclic quadrilateral. A tangent PQ is drawn on the point B of the circle. If ∠DBP = 65⁰ then find ∠BCD-

ABCD एक चक्रीय चतुर्भुज है। एक स्पर्श रेखा PQ वृत्त के बिंदु B पर खींची गई है। यदि ∠ DBP = 65⁰ तो ∠ BCD ज्ञात कीजिये-

(A) 105^o

(B) 115^o

(C) 125^o

(D) 95^o

Sol. – (B)

∠DBP = ∠DCB = 115^o (alternate angle/एकान्तर कोण)
∠BCD = 115^o

Q.7 – Two chords AB and CD of a circle intersect at E such that AE = 2.4 cm, BE = 3.2 cm, and CE = 1.6 cm. The length of DE is-

एक वृत्त की दो जीवा AB और CD, E पर इस प्रकार प्रतिच्छेदित करती है कि AE = 2.4 सेमी, BE = 3.2 सेमी और CE = 1.6 सेमी. DE की लम्बाई क्या है?

(A) 1.6 cm/सेमी.

(B) 3.2 cm/सेमी

(C) 4.8 cm/सेमी

(D) 6.4 cm/सेमी

Sol. – (C)

AE × BE = CE × DE
2.4 × 3.2 = 1.6 × x
x =  = 4.8 cm. /सेमी

Q.8 – The areas of two similar triangle are 12 cm² and 48 cm² . If the height of the smaller one is 2.1 cm, then the corresponding height of the bigger one is-
दो समरूप त्रिभुजों के क्षेत्रफल 12 सेमी² और 48 सेमी² है यदि छोटे त्रिभुज की ऊँचाई 2.1 सेमी है तो बड़े त्रिभुज की संगत ऊँचाई क्या है?

(A) 4.8 cm/सेमी

(B) 8.4 cm/सेमी

(C) 4.2 cm/सेमी

(D) 0.525 cm/सेमी

Sol. – (C)

Q.9 – 10 years ago Ram was 5 times as old as Shyam but 20 year later from now he will be only twice as old as Shyam. How many years old is Shyam?

10वर्ष पहले राम, श्याम से आयु में 5 गुना था, लेकिन अब से 20 वर्ष बाद वह, श्याम की आयु का केवल दोगुना होगा। श्याम की आयु क्या है?

(A) 20 years/वर्ष

(B) 30 years/वर्ष

(C) 40 years/वर्ष

(D) 50 years/वर्ष

Sol. – (A)

Let the present age of Ram and Shyam be x and y years./माना राम और श्याम की वर्तमान आयु x और y वर्ष हैं |

(x – 10) = 5 (y – 10)
x – 5y = – 40 ________(I)
and/और (x+20) = 2(y+20)
x – 2y = 20 _________(II)
On solving/हल करने पर,
y = 20 years/वर्ष

Q.10 – When x⁴⁰ + 2 is divided by x⁴ +1, what is the remainder?

जब x⁴⁰ + 2 को x⁴ +1 से भग दिया जाता है तो शेषफल क्या है?

(A) 1

(B) 2

(C) 3

(D) 4

Sol. – (C)

Let/माना f(x) = x⁴⁰ + 2
 Put/रखिये x⁴ = –1,
 f(x) = (–1)¹⁰ + 2 = 3

Answers:

Q1. (A)

Q2. (D)

Q3. (B)

Q4. (C)

Q5. (D)

Q6. (B)

Q7. (C)

Q8. (C)

Q9. (A)

Q10. (C)